理系学部の学部生のためのサイフォンの原理
サイフォンと滑車と説明と
まず「サイフォンを動かしているのは重力」という表現について検討を加えよう。
これはサイフォンが動作することによって、高いところにあった流体の位置エネルギーが運動エネルギーに変わっていくプロセスだから、「重力によって動く」という表現もあながち間違いではない。しかしこの説明では、容器を単純にパイプで繋いでも同じことが言えるので、サイフォンが一旦、高いところに流体を持ち上げてから下ろすというサイフォンの特徴の説明にはならない。
諸君は高校の物理の時間に「滑車」の問題を解かされた経験があるだろう。滑車も両側のおもりの持つ位置エネルギーを運動エネルギーに変えているわけだから、「滑車を動かしているのは重力」と言っても差し支えない。けれども、これで「滑車の運動を解いた」と言えるだろうか?諸君は両側のおもりのそれぞれにかかる重力と張力の大きさを検討し、それらの差からおもりに生じる加速度を計算したはずだ。おもりの質量差が小さいほど、滑車はゆっくりとうごいたはずだ。運動をきちんと理解するためには、運動方程式に立ち戻って、各部にかかる力をきちんと検討すべきである。
『サイフォンは「大気圧」か「重力」か?』の議論がいま巷を賑わしているが、ナヴィエ・ストークス方程式に基づいて、サイフォンの各部分の流体にどのような力がかかっているのかを検討をしよう。
ナヴィエ・ストークス方程式
ニュートンの運動方程式は m a = f1 + f2 + f3 + … で与えられるが、これを流体の運動に当てはめ、速度場の時間変化の式に書き換えると、ナヴィエ・ストークス方程式
∂tu + (u・∇)u = - ∇p/ρ + g + ν△u(νは動粘性係数)が得られる。流体の運動をオイラー的に記述する立場では、流体の加速度は ∂tu + (u・∇)u で与えられる。この方程式で仮定したことは、流体の各部分にかかる力として
- 圧力勾配:f1/m = -∇p/ρ
- 重力:f2/m = g
- 粘性による摩擦力:f3/m = ν△u
まず方程式の細かい計算をする前に、日頃使っているサイホンがどの程度のものなのかを見ておこう。ここではポリタンクから石油ポンプを使って石油ストーブのタンクに石油を入れるのが、どの程度の大きさのものなのかを見積もる。オーダーとして ρ g h 〜 1000[kg/m3] × 10[m/s2] × 0.2[m] = 20[hPa] となる。じゃあ 20 hPa 程度の流れってどれくらいの速さなんだろう。ρ v2/2 = 20 [hPa] なので v = 2 [m/s] となる。2 [m/s] ってどれくらいの速度かというと、石油ポンプの管の長さが 1[m], 断面積が 1 [cm2] = 0.0001 [m2] くらいとすると、0.0002 [m3/s] = 0.2 [L/s] くらいの流量。これで 18 [L] の石油缶を満たそうとすると 90 [s] で給油が完了する。
さてさて、ここに出てくる「圧力」の次元を持つ量の大きさは大体 10 [hPa] のオーダーだ。これに対して大気圧は 1000 [hPa] のオーダーで2桁くらい値が違うから、石油缶の問題で流体の方程式を解こうと思ったら、まずは静水圧平衡での圧力の分布を計算しておいて、そこから流れの影響の部分を補正として計算する…という計算手順になるだろう。
ナヴィエ・ストークス方程式を解く
ナヴィエ・ストークス方程式を次の仮定の下で解く(線形な釣り合いの式として考えたいの言い換え)
- 大気圧、流体の密度は一定。
- サイフォンの両端の容器の水位は変化しない。*1
- サイフォンの両端の管口の圧力は周辺の流体の静水圧に等しい。*2
- 流れは一定(にきわめて近い):∂tu 〜 0
- 流れは管軸方向を向いているので、非線形項の大きさは他の項に比べて小さい*3:|(u・∇)u| ≪ |∇p/ρ|, |g|, |ν△u|
0 = - ∇p/ρ + g + ν△uとなる。*4
[2013.12.19追記]以上の前提条件は「流れがとてもとても遅い状況を考えている(だから層流解がパイプ内で第1近似として期待できる)」ということである。だから管内のレイノルズ数が1000に満たないような状況でしか適用できない。*5
線形化しているので解の重ね合わせの原理が数学的に成り立つ。つまり圧力を二つのパートに分解して、その全体が境界条件を満たすように解けばよい。*6
そこでまず重力と圧力の間に釣り合いがあるとして
0 = - ∇pstat/ρ + gで pstat を解き、pstat からのズレを
0 = - ∇pflow/ρ + ν△uで解く。ここで得られた pstat と pflow の和が流体にかかる圧力である。解く時の境界条件は
p(inlet) = patm + ρ g D1, p(outlet) = patm + ρ g D2となる。
ここで気をつけなくてはいけないことがある。静水圧の式は関数 p の1階の微分方程式なので境界条件は1個しか要らない。その一方で粘性摩擦の式は関数 u の2階の微分方程式なので、解くためには境界条件が2個必要になる。
まず pstat を解く。重力がz-方向下向きにかかっているとして、方程式は
∂pstat/∂x = 0, ∂pstat/∂y = 0, ∂pstat/∂z = - ρ gとなる。この方程式*7は流体にかかる圧力は高度に比例して減ることを意味している。
高水位側の管口 inlet の高度を z=0 とおいて、この方程式を積分すると
pstat(x,y,z) = - ρ g z + patm + ρ g D1となる。この結果を使って、管の各部の pstat を求めると以下のようになる:
pstat(inlet) = patm + ρ g D1
pstat(highest) = - ρ g ( D1 + HS ) + patm + ρ g D1 = patm - ρ g HS
pstat(outlet) = - ρ g ( D1 + HS - HS - HD - D2) + patm + ρgD1 = patm + ρ g ( HD + D2 )
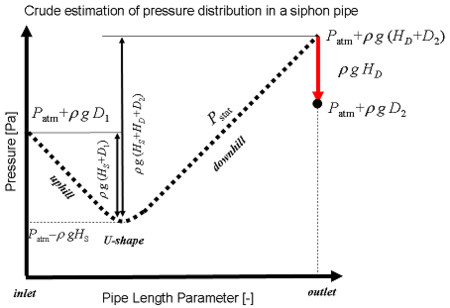
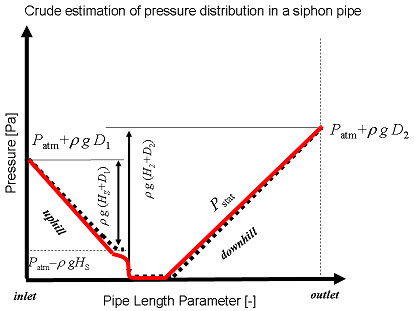
静水圧 pstat の分布の概形は右図のようになる。ところでこのときの pstat(outlet) の値は出口側の管口部の実際の圧力の値 p(outlet) と食い違っている(右図の赤い矢印で示したギャップ)
p(outlet) - pstat(outlet)つまり静水圧平衡で計算した値と実際の圧力の食い違いの大きさは ρgHD である。計算で得られた pstat の値はこの本当の圧力 p と食い違っているが、食い違いの値は管口の水深、パイプの高度には関係がなく、両サイドの容器の液面の高さの差で決まっている。
= ( patm + ρ g D2 ) - ( patm + ρ g ( HD + D2 ) )
= - ρ g HD
ここからいえることは、流体が動く理由は、圧力の食い違いなので、流体の管内の流れを説明するのに、管内の流体にかかる重力を使って説明する方式は、定量的な説明ができない…というか、間違い。
さて、この食い違いの部分をナヴィエストークス方程式の残りの部分で解く。つまり
0 = - ∇pflow/ρ + ν△uを境界条件
pflow(inlet) = 0, pflow(outlet) = - ρ g HDのもとで解く。この式の意味は管内の流体にかかる重力は管内の流体の流れの強さの計算には出てこないということである。
この方程式の解はパイプの形状によって千差万別である。しかし、
どのような形状のパイプであろうと、またパイプの両端がどのような水深にあろうと、流れを駆動している圧力差の大きさはサイフォン両端の液面の高度差のみで決まっている。これはサイフォンが重力ポテンシャルを解放する装置であるという当初の考察を補強している。
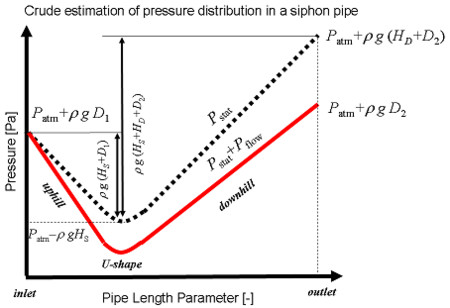
これを考慮に入れると管の内部の圧力の分布 p は右図の赤い実線のようになるだろう。この図では管の径が一様で圧力損失が一様だとした。この圧力のうち流体の流れを決める部分は点線と実線の差の部分であり、点線の部分は重力との静水圧平衡に使われる。つまり大気圧を流れの動力源とするような説明は妥当ではない。
ここで「流れの動力源」はナヴィエ・ストークス方程式の流れ u を決める部分の式 0 = - ∇pflow/ρ + ν△u を積分するときのパラメーターを検討すればわかる。密度 ρ、重力加速度 g、液面の高度差 HD は流れ u の解を求めるときに、境界条件としてパラメータに入っているが、大気圧 patm は入ってこない。これより大気圧が2気圧だろうと3気圧だろうと、流れが2倍、3倍と早くなるわけではないことがわかる。これが大気圧を流れの動力源とするような説明は妥当ではないと述べた根拠である。*8
このことは同時に管内の流体にかかる重力を流れの動力源とする意味になる説明も妥当ではないことを意味している。というのも、境界条件に入るパラメーターである HD はサイフォンの外側にある流体にかかる重力に関わるパラメーターであるからである。エネルギーに関する考察の部分で述べたように、管の外の双方の容器内の流体の重力ポテンシャルの差が流れの動力源である。
分からず屋のための力の釣り合い入門[この節は2010.6.13追記]
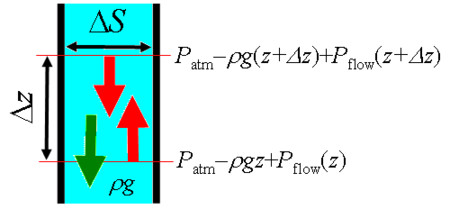
流体の微小要素にかかる力の大きさを見てみよう。サイフォンのパイプの中の高さ z の位置にある断面積ΔS, 厚みΔzの微小要素を取り上げよう。ここで z の位置は流入側(上昇側)にとり、z=0 が流入側の液面になるようにとる。微小要素の下面(高さz)では
- 上向きに(図の赤い上向きの矢印)
- pstat = patm - ρ g z
- pflow(z) これは管の形状で変わる
微小要素の上面(高さz+Δz)では「この面より上の液体がのしかかってくる」ので
- 下向きに(図の赤い下向きの矢印)
- pstat = patm - ρ g (z+Δz)
- pflow(z+Δz) これは管の形状で変わる
これらの圧力が断面積ΔSにわたってかかっているので、微小要素にかかる力のうち圧力の寄与は
Fpres = ( pstat + pflow )(z+Δz)×ΔS - ( pstat + pflow )(z)×ΔSとなり、patm はどこにも表れない。流体にかかる力を計算したら patm は計算の結果として、全く現れないのだ。これがボクが「大気圧を動力源とする説明は間違い」と言い続ける根拠である。微小な要素に着目して patm が現れないのだから、当然、これを積分したサイフォン管の内部の流体全体になされる仕事にも patm は現れない(普通のサイフォンは深さ、高さを10mよりは十分小さい範囲で使うからね)。「大気圧が仕事をする」なんて議論する奴の気がしれない。
= - ρ g Δz ΔS + ( pflow(z+Δz) - pflow(z) )×ΔS
重力の寄与は Fgrav = ρ g (ΔS×Δz) であり(図の緑の矢印)、これは Fpres の - ρ g Δz ΔS と打ち消しあう。すなわち重力と圧力がこの微小要素にかける力の総和は
Fpres + Fgrav = ( pflow(z+Δz) - pflow(z) )×ΔSである。これがボクが「管内の流体にかかる重力を動力源とする説明は間違い」と言い続ける根拠である。
この計算結果の意味は何か?それは大気圧は流体を動かさないし、ρ g z の部分も重力と釣り合うので流体を動かす力ではありえないということだ。これは静水圧平衡の式の解なので当然だ。
では大気圧の役割は何かをもう少し詳しく検討しよう。静水圧平衡を考えればわかるように流体の圧力は負にはなりえない。流体の圧力がゼロとなる高度で液柱は尽きる(たとえば1気圧下の水銀ならz=760mmである)。これを式で表すとpstat + pflow = patm - ρ g z + pflow(z) > 0
となる。この式の意味は大気圧 patm の役割は p>0 となる z の高度を決める境界条件に過ぎない。すなわち大気圧 patm の役割はサイフォン内部の流体を(動かすことではなく)静かに下から支えることであり、これが大きければ支えられる高さが高くなるということ
に過ぎない。運動方程式の解をきちんと分析したら大気圧って「水が落ちないように静かに支える」だけなんだ。「大気圧が仕事をする」なんて議論する奴の気がしれない。結局、流体の流れに直接に寄与する力は「液面の高度差で決まる圧力勾配」の項 ( pflow(z+Δz) - pflow(z) )×ΔS しか残らない。そしてこれが粘性散逸と釣り合っていて、全体として定常な流れができるのである。だからサイフォンの動作を理解しようと思ったら、圧力の勾配の源である、圧力のギャップがどことどこの間に生じるかを分析すればよいということなんだ。そしてまたボクは(大気圧ではなく)管外の液体にかかる重力が仕事をするという表現ならば、納得(あるいは許容)するだろう(よっぽどヘンテコなサイフォンを考えているんじゃなければね)。
その一方でサイフォンの管内の微小な要素に着目した議論において、大気圧が全面に出る説明が出たならば、眉に唾をつけて聞くことをおすすめする。
大気圧の寄与に関する重要な注
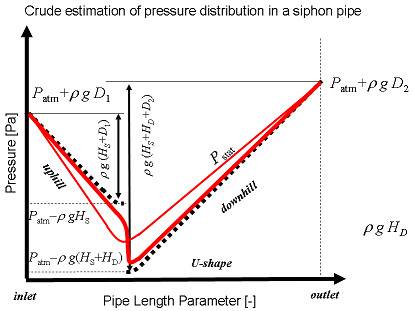
ここで赤い実線のグラフを見てみよう。グラフの最下点が流体にかかる圧力が最も下がる部分である。この最下点の値が 0 [Pa] に近い値まで下がっていたらどうなるだろう。これが「10mサイホン」の挙動を考える上でのキモになる。
もしここでこの点の高さがこの環境温度での水蒸気圧より低ければ、管内で「沸騰」が起こるだろう(cf. http://www2.hamajima.co.jp/~tenjin/labo/siphon.htm)。
さらに重要な点はグラフの主要な点の座標にはすべて patm が付いている。つまり大気圧はサイフォンが動作するかどうかを決める重要なオフセット・パラメーターになっている。だから patm を徐々に下げるような実験をすると、サイフォンが効かなくなる現象を見ることができるだろう。
重力の寄与に関する重要な注
重力は流体要素の各小片において上下方向に一様にかかっているので、重力は流体要素を引き伸ばしたり、縮めたりするような力の寄与をしない。
サイフォンいろいろ[2010.6.14追記]
分からず屋モデルを検討してみる。
モデル1
頂点にバルブを入れてみる(左図)。バルブを完全に締め切ったときの圧力分布は右図の点線。この点線の計算は静水圧平衡の式 -∇pstat/ρ + g = 0 の式を連続性が成り立っている範囲で計算する。つまりバルブの左側では pstat(inlet) = patm + ρ g D1 を境界条件として、右側では p(outlet) = patm + ρ g D2 を境界条件として積分する。
バルブをちょこっと開けると、左右の圧力ギャップ ρ g HD を解消しようと流れ始める(図の赤い太線)。この図の解釈は
バルブ内とバルブの前後は圧力勾配が大きく、激しい流れができている。でもバルブはほとんど閉まっているので、流速は大きいけど、流量は小さい。流量が小さいのでパイプの部分の圧力は静水圧からほんのちょこっとだけしかズレない。でも、この静水圧からのずれが pflow であり、これが管内のゆっくりとした流れを引き起こしていることは言うまでもない。
もしバルブを全開するとギャップの解消は管の全体で起こる(図の細い赤線)。これは上で解説したものと同じ。
全閉状態(図の点線)から全開(図の細い赤線)まで圧力グラフは徐々に変化する。
流れが解消しようとしている圧力のギャップの値は「ちょこっと開けた状態」でも「全開状態」でも ρ g HD であり、これには大気圧 patm は絡んでこないので、流れは大気圧によって作られるとは到底、言い難い。
モデル2
頂点にバルブを入れ、かつ、サイフォンの全体を圧力容器に入れて大気圧を徐々に減らすと、うまく設定すればバルブの右側にトリチェリ真空ができる(だから静水圧平衡のグラフは途中で 0[Pa] を這っている)。点線の計算は上のサイフォンと同じだが、右側ではサイフォンの頂点に辿り着く前に pstat(z)=0 となり、ここで流体力学的に扱える範囲は終わる。
バルブを開けると左側の液体がこぼれ落ちる。こぼれている最中は 0[Pa] の環境にあるので、圧力 p=0 [Pa] で運動方程式は g の項のみが残る、いわゆるフリー・フォール状態になる(だから流体力学的考察は要らない)。落ちた後は水柱は0気圧の高さよりは微妙に高いはずだから、水は徐々に右のパイプから押し出される。(だから赤線は点線よりも微妙に上に描いた。でも、この静水圧からのずれが pflow であり、これが管内のゆっくりとした流れを引き起こしていることは言うまでもない。)
で、ヘンテコな形だけれど、これもサイフォンとして機能している。では、サイフォンの機能の原因である圧力ギャップを計算しよう。この場合はバルブの左右を比較すると pflow = patm - ρ g HS で大気圧の値が陽に出てくる。
だからこの「低圧下(真空付き)サイフォン」なら、大気圧の変化で流量の変化が起こる。これなら「流体の運動の原因として大気圧も考えられる」と結論していいだろう。実に興味深いモデルだ。
しかし環境の圧力を徐々に上げていったらどうなるだろう。結局は上のサイフォンに戻ってしまうし、戻ったとたんに pflow の原因となるギャップの値は ρ g HD になるのであり、大気圧の値は関係なくなってしまう(もちろん戻った瞬間だけは pflow = patm - ρ g HS = ρ g HD となっているんだけどね)。
だからこんなヘンテコなサイフォンから変化をさせていって、通常のサイフォン、例えば石油ポンプを説明できるなんて考えている奴はイカレているとしか言いようがない。(ちゃんと圧力分布を解いてグラフ化してみろよ。)
*1:容器がそれなりに大きい、あるいは水流がそれなりに遅いという程度の意味。
*2:本当は管口の周辺では吸い込み・吐き出しの流れがあるから微妙に違うんだけど、そんなに極端には違わないという程度の意味。
*3:これは式を解いた後で、再帰的に解を代入して値が小さいことを確かめる必要がある。
*4:もちろん流れが複雑で乱流だったりとかしていても「圧力」pを流体の本当の圧力ではなく、乱流なんかにより生じる「圧力損失」まで組み込んで考えているんだという考え方もあり得るだろう。
*5:流体力学の研究をすれば、この前提、この近似が「やたらに遅い流れ」の言い換えだというのは自明だと思って、ここに書かなかったことを大変、後悔している。
*6:場の量のいくつかを境界条件を満たすような2個以上の場に分解して解く手法は数値計算ではよく用いる基礎的な手法である。
*7:この式が成り立つ状態を静水圧平衡という
*8:この段落 2010.6.12 追記。