サイフォンの原理とそれにまつわるいくつかの誤概念について
サイフォンの原理とは
ということである。オッカムの剃刀の原理(対偶を取ると「いらんことを言うと、話がややこしくなる」)に則ると「圧力がかかるから液体が流れる」という説明でサイフォンの原理は十分なのではないか。無理して「保存則がどうたら」とか言わない方がいいんじゃないか。
サイフォンの誤概念のリスト
ボクが目にした範囲内のものを列挙してみる。一応「反証実験」も考えたが、自説にこだわる人の手にかかれば、あっさりと「反論」されるかもしれない:
- 大気圧が管内の流体を押して動かしている
[ウソ]管の中に「仕切り」を入れて仕切りにかかる圧力差を求めたときに、大気圧はパラメーターとして入ってこない
[反証実験の提案]周辺の大気圧を2気圧とか0.5気圧とかに変えて、流量に差が出るか調べる。
[注意]大気圧がサイフォンに無関係だという話ではない。「サイフォンが可能な高さは大気圧で決まる」というのは正しい。これはNHKが『大科学実験』という番組で、水を使ったサイフォンが10mで途切れること、上流側の圧力を上げるとサイフォンの高さも上がることを実験で実証してくれている。 - 管の内部の流体に重力がかかっていて、それが動かしている
[ウソ]これも管の中に「仕切り」を入れて仕切りにかかる圧力差を求めたときに、管内部の流体にかかる重力はパラメーターとして入ってこない。管の外の容器内の流体にかかる重力が押している。
[反証実験の提案]上昇する部分の長さが長くなるサイフォンを作って、動作することを確認するとか、出口の部分を上に向けるとか、サイフォンの形をいろいろに変える。 - 流体が鎖のようになって引っ張っている
[作動流体が水のようなニュートン流体ならばウソ]ニュートン流体は剪断応力に対する復元力を持たないので、引っ張ったら引っ張られっぱなしで、コンニャクみたいにゆがみを元に戻そうとすることはない。
[非ニュートン流体だったらOK]実際にそんな実験ができるようなゲルが教材として売られている。
[反証実験の提案]「水」サイフォンと「ゲル」サイフォンを減圧できる状況下に置いて、減圧すると「水」サイフォンの管内の水が途切れることを確かめるとよい。実験装置の形状は同一であるから流体が内部の「分子間の鎖の力」で引っ張っているならば、周囲の圧力に依らず引っ張って支えている力が継続してかかっているであろうから。たぶん「ゲル」サイフォンは切れない(と思うけど、低圧環境下でゲル分子間の溶媒が蒸発して粘弾性が変わるみたいなこととか起こらないかちょっと心配)。 - ベルヌーイの定理でサイフォンが動作する理由を説明できる
[ほぼほぼウソ]ベルヌーイの定理は[1]定常流において[2]単一の流線に沿って流体の運動を追跡すると[3]流線上のどの点においてもベルヌーイ関数 B = ρ u^2/2 + p + ρg z が保存するという定理だが、サイフォンの問題において[1]きちんと流線を管の両端につながる容器から引っ張ってきて、[2]その全線において圧と速度のバランスを考察した上で、管内の流れの生成を説明したものが(特殊なセットアップを除いて)ない。これについては理論の適用状況をピトー管、霧吹きと比較して考察する。 - サイフォンの流量計算にベルヌーイ式が使える
[OK]「ベルヌーイ使えるじゃん」とおっしゃっている方々の説明の共通点として、「管の両端に圧力差 ρ g H がある」ことを前提として、ベルヌーイ式で流入口、流出口の損失や管摩擦(多分、粘性散逸と乱流による圧力低下)の影響まで考慮に入れて、管内の流量を計算しておられる。この計算は管に ρ g H の値の能力を持つ電動ポンプを繋いでも同じ計算である。これは「ポンプとパイプの組み合わせの性能の見積もり」であって、液面の高さに差のある二つの容器を強制的に管でつないだときに生じる圧力差がなぜ ρ g H という値になるのか、なぜこんなシンプルな装置で「ポンプができあがる」のかの説明にはなっていない。
「ベルヌーイの定理」のロジックの検討
サイフォンへの「ベルヌーイの定理」の適用を検討する前に、高レイノルズ数でありながら「ベルヌーイの定理」すなわち流線に沿った物理量の保存を用いた概算がうまくいく二つの例(ピトー管、霧吹き)を検討してみよう。
ピトー管の場合には非常に近い2本の流線を考慮している。この2本の流線の上流側の境界条件を p0, v0 とする。一方の流線はピトー管の正面で静止状態になり、流線は淀み点を端点として持つ。したがってピトー管正面の圧力 ps は p0 + ρ v02/2 = ps で概算できる。もう一つの流線はピトー管が大気の流れと平行な向きなので、ほぼ v0 のままと考える。すると管正面と管側面の圧力差から対気速度が推定できる。もちろん現実の航空機では高レイノルズ数の流れなので、ピトー管の周囲には剥離流れや乱流境界層が必ず出来ているけれども、オーダーを知るための概算には十分だ。
このピトー管の検討の要点は[1]物理量を比較する流線がはっきりと定義されていること、[2]流れがピトー管の影響を受けるより十分に前の状態を上流側の境界条件として採用していること。
つぎに霧吹きの例(種子田(1995)*1)を検討する。種子田の指摘は、霧吹きで水の吸い上げを説明するときに、適切な装置の位置関係と流線を選択しないといけないということだ。種子田は上流側に接続するぎりぎりの流線として、霧吹きの口の角の剥離点に向かう流線を選択している。
この例で重要なことは、[1]系の幾何学的形状から流れを事前に推測することが可能なこと、気流の吹き出しが水管にぶつかることで流線に沿って気流の加速が起こる(だから結果として圧力減少がおこらないといけない)ことが予めわかること*2、[2](反面教師的だが)幾何学的配置や流線の選択をミスっても初学者をだませる程度の「ロジック」をつくることができるということだ(これが種子田先生が解説記事を書いた動機なのだろう)。
さて話をサイフォンに移そう。サイフォンとしては十分に大きな2個の流体の容器をパイプで繋いだものを考えよう。
サイフォンの原理が「ベルヌーイの定理から導かれる」としたら、つぎのようなロジックになるだろう;
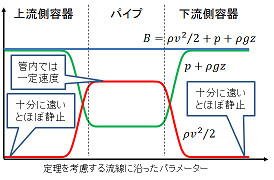
流体の容器も含めた系の全体を考え、その中で[1]管口から十分に上流側から始まり、サイフォン管の中を通って、十分に下流側へと延びる適切な流線を考えると、[2]その流線上で B:= ρv2/2 + p + ρ g z (vは流線上の速度の大きさ、pは静水圧、zは基準高からの高さ)は一定値をとるから、Bの各項の大きさを考えたときに、[3]管の内部では p + ρ g z が流線の上流側、下流側の境界条件の値よりも低くなるということが装置の形状等の外的な条件から言えるから、管の内部にその減少分を補うだけの速度が生じていなくてはならない(だから流れる)。
まず[1]の「流線」の問題を検討しよう。
ベルヌーイの式が使える(だから「ベルヌーイの定理で動作を説明していいんじゃない?」)とおっしゃる方々に共通する点として、管の両端に ρ g H の圧力差が生じることを前提として計算をしていらっしゃる。この ρ g H をきちんと定量的に評価できるためには、どのような流線を選択しないといけないであろうか。
流線は液面の高さの情報を含まねばならないので、上流側の容器の液面から始まり、パイプを通って、下流側の容器の液面にたどり着く流線をとらないと静水圧の情報を引っ張ってこれない。(もしこの流線が不自然だと思うならば p と ρ g z をまとめて p + ρ g z で扱えば、流線の端点の水深は自由に取れる。)
つぎに[2]の流線に沿った保存量の検討に移ろう。
いまサイフォンとして両側の容器とも十分に大きな容積を持っていると仮定する。するとサイフォン管から十分に離れた部分では u が十分に小さくなる。粘性で散逸する量が小さいとしても、容器が十分に大きければ非圧縮性の条件から u は大雑把に見積もって r-2 (rは流体の管口からの距離)で小さくなることが期待できる。このとき管口から十分遠方ならば u は十分に小さいと期待できるので、流線に沿った B の境界値として、それぞれの容器内の静水圧平衡の値を B の値に取っても、サイフォンの動作を見積もるための概算には十分だろう。
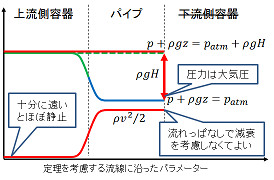
それではパイプ内の流体にかかる圧力の値と、ベルヌーイの定理の考察に必要な流線に沿った B の値の上流側、下流側の境界値を見積もってみよう。図のようなサイフォンを考え、z=0 を低液面側の液面高にとり、各容器で液面での圧力が大気圧 patmに等しいとして、圧力を評価してみる*3。
上流側の口を塞いで流れをピタッと止めて、圧力+重力を流線に沿って評価すると、指の上流側にかかる圧力が p = patm + ρg D1, 下流側にかかる圧力が p = patm + ρg ( - H + D1 ) となって圧力のギャップ ρg H ができる。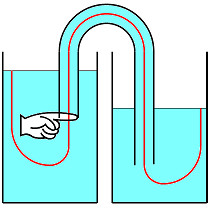
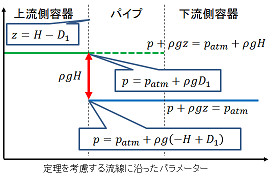
下流側の口を塞いで圧力+重力を流線に沿って評価しても圧力のギャップ ρg H が指の両側にできる: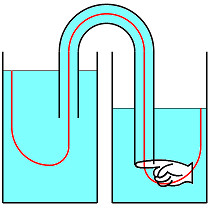
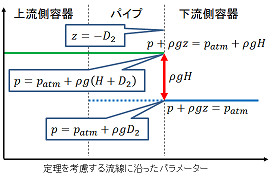
管の最高点を塞いでも圧力+重力を流線に沿って評価しても圧力のギャップ ρg H ができる: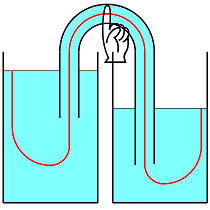
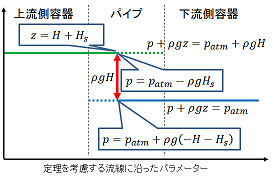
というわけで流線に沿った B の値の境界値を見積もると、上流側で p + ρg z = patm + ρg H, 下流側で p + ρg z = patm となってしまい、十分に遠方で u が小さくなる場合には流線に沿った保存量 B を想定できないというのが、ボクが「ベルヌーイの定理でサイフォンの原理を説明できない」と主張する第1の根拠。ベルヌーイの定理を主張するなら、上流から下流までの流線を全線考えてから主張すべきじゃないだろうか。(松田先生の例は4段落下で言及している。)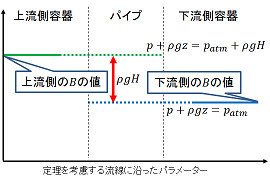
ちなみに「サイフォンにベルヌーイの定理が使える」という主張は大抵の場合、図に描いたような流線を陰に想定して静水圧平衡の情報を管口に引っ張ってきた上で、上流側の B と下流側の B に ρg H のギャップがあるから、このギャップを「運動エネルギー」と「圧力損失(水頭)」としてベルヌーイの式を用いて概算して、流量を求められるという意味で使っている。これはただの「ポンプとパイプの組の能力計算」に過ぎないのであって、きちんと「定理の保存量が境界条件も含めて流線全部で考えられる」と主張したものを(少なくともあらきのサイフォン関連エントリのコメント等では)見たことがない。
次にベルヌーイの定理が適用可能なら、「サイフォンの幾何学的形状から管内の圧力が下がると事前に分かる」ので、結果として「管内の流速が上がる」と推論できるだろうか。
ピトー管、霧吹き(さらにはベンチュリー管も)の例では「系の幾何学的形状から、流線に沿って追跡すると流速が上がる」から、結果として「流線に沿って圧力が下がる」という結論を出している。サイフォンを説明しようとすると、ちょうどこの逆の「系の幾何学的形状から、流線に沿って追跡すると圧力が下がる」から、結果として「流線に沿って流速が上がる」と推論しなくてはいけないはずだが、[1]流線に沿って保存量 B の値を与え、かつ[2]圧力が下がるという推論を、一般のサイフォンでできるのだろうか?(一般にはできそうな気がしない。)
ではどのようなサイフォンでも説明できないかというと、できそうな例も作ることができる。下流側の「プール」をバッサリと消してしまい、管の先端を大気に開放している場合だ。これは境界条件として下流端を大気中に開放して、無理やり境界条件を大気圧 patm にして、そこから先では「だだ漏れ」だから流れの減衰も考慮しなくてよい。この境界条件なら、形状だけからベルヌーイの定理を用いて流れが発生するという結論が出てもいいと思う。(ただし現実のサイフォンでは低レイノルズ数でも高レイノルズ数でも粘性の影響が無視できないから p を単純に「圧力」と解釈できない。これについては後述する。)

でも、水のたっぷり入った2個のバケツをホースで繋いでもちゃんとサイフォンとして動作するから、この「下流バケツ切り捨てモデル」のセットアップではサイフォンとしての一般性が無い(ように、少なくともボクは感じてしまう)。批判の要点は、パイプよりも下流側での流れの状態を大気中への自由流出にしてしまうのは、適用可能性の狭い設定ではないかということだ。ベルヌーイの定理は上流から下流まできちんとつながった流線上のすべての点で成り立たないといけないから、下流側の設定で変わるような一般性の無い「動作原理の説明」は避けるべきだと思う。
以上の議論よりベルヌーイの定理で説明しようとすると、[1]流線の両端で p + ρ g z の値が食い違うので定理の保存量が設定できない、[2]サイフォンの形状だけから管の内部での圧力の減少を説明でき(そうな例もないわけではないが、一般の形状ではありそうにも)ないという2点でサイフォンの動作原理としてはまずいのではないかと思う。特に1番目の流線に沿った保存量が無いというのは「ベルヌーイの定理って言うな!」と叫ぶのには十分な理由になると思う。
実際のサイフォンでは、この流線に沿って p + ρ g z を評価すると、必ず両端で ρ g H のギャップが発生するので、流体はその圧力のギャップに押されて流れる。流線に沿った圧力は、流体の加速、粘性によるエネルギー散逸、乱流の発生の結果として、上流側の値から下流側の値に向けて減少していく。「なぜ流れるか?」に対する説明にはこれで十分ではないか?「どれだけ流れるか?」という問題と混同してはいけないのではないか?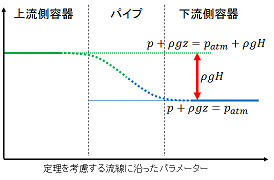
ベルヌーイの定理の導出
ベルヌーイの定理もベルヌーイの式もサイフォンの原理に比べれば、流量計算のためのわき役に過ぎないので気乗りがしないが、これらの式を導出して、考察をしよう。
「定理」の出発点はオイラー方程式
となる。ここで流体が非圧縮性
∂tu = -∇( p/ρ + g z + |u|2/2 ) + u×curluとなる。ここで速度場が定常 ∂tu = 0 という条件を課した上で、流線(定常なベクトル場 u の積分曲線)に沿って評価すると、u×curluはuに垂直なので消えて
∂s( p/ρ + g z + |u|2/2 ) = 0という式が導かれる(sは流線に沿ったパラメーター)。これを流線に沿って積分してベルヌーイの定理
∫s0s1∂s( p/ρ + g z + |u|2/2 ) = 0(s0, s1は同一流線上で上流側、下流側のどこか)が導かれる。
⇒ (p/ρ + g z + |u|2/2)s=s1 - (p/ρ + g z + |u|2/2)s=s0 = 0
ここで積分後の式を考えよう。流速 |u|2/2 が大きいところは、圧力+重力 p/ρ + g z が低い。この結果をバケツを繋いだサイフォンに適用すると、「流体はパイプとその周辺だけ流れているから、ベルヌーイの定理が適用できるならば、パイプとその周辺だけは圧力+重力 p/ρ + g z が下がるし、それから遠くなると流速 |u|2/2 がなくなるから、圧力+重力 p/ρ + g z は下流側で上流側と同じ値に戻らないといけない、というロジックになる(もちろんこれは現実のサイフォンではあり得ない)。
ベルヌーイの定理から言えることは「同一流線上で速度が速い部分では圧力が低い」であって、「下流側の圧力が低いから流れる」という話とベルヌーイの定理を結びつけるのはかなり強引で危なっかしい話だと思う。
ベルヌーイの式の導出
「ベルヌーイの式」の導出はベルヌーイの定理よりも概念的、計算的にちょっとだけ複雑である。
「式」の出発点はナビエ・ストークス方程式
(⊗ はテンソル積の記号)である。この式では圧力項と非線形項のテンソル積への書き換えで、非圧縮性 ρ=(一定) を仮定している。これを乱流状態まで想定したうえで式変形をする。まず速度場 u, 圧力場 p を「(アンサンブル)平均*4」U, P, と「揺らぎ」u', p' に分解したものを代入しよう:
これの平均を取ると(括弧〈*〉で表す)
![=-\nabla[(P+p')/\rho]](https://chart.apis.google.com/chart?cht=tx&chl=%3D-%5Cnabla%5B%28P%2Bp%27%29%2F%5Crho%5D)

![- \nabla\cdot[(\boldsymbol{U}+\boldsymbol{u}')\otimes(\boldsymbol{U}+\boldsymbol{u}')]](https://chart.apis.google.com/chart?cht=tx&chl=%20-%20%5Cnabla%5Ccdot%5B%28%5Cboldsymbol%7BU%7D%2B%5Cboldsymbol%7Bu%7D%27%29%5Cotimes%28%5Cboldsymbol%7BU%7D%2B%5Cboldsymbol%7Bu%7D%27%29%5D)
「平均」の定義より 〈u〉=〈U + u'〉= U, 〈p〉=〈P + p'〉= P, 平均と揺らぎの積の平均はゼロとなることを用いると
![=-\left<\nabla[(P+p')/\rho]\right>](https://chart.apis.google.com/chart?cht=tx&chl=%3D-%5Cleft%3C%5Cnabla%5B%28P%2Bp%27%29%2F%5Crho%5D%5Cright%3E)

![- \left<\nabla\cdot[(\boldsymbol{U}+\boldsymbol{u}')\otimes(\boldsymbol{U}+\boldsymbol{u}')]\right>](https://chart.apis.google.com/chart?cht=tx&chl=%20-%20%5Cleft%3C%5Cnabla%5Ccdot%5B%28%5Cboldsymbol%7BU%7D%2B%5Cboldsymbol%7Bu%7D%27%29%5Cotimes%28%5Cboldsymbol%7BU%7D%2B%5Cboldsymbol%7Bu%7D%27%29%5D%5Cright%3E)
となる。
∂tU = -∇( P/ρ + g z + |U|2/2 + ν∇⊗U + 〈u'⊗u'〉 ) + U×curlU
この式は「レイノルズ平均ナビエ・ストークス方程式 (Reynolds averaged Navier-Stokes equation, RANSと省略される)」と呼ばれている。
ここで「ベルヌーイの定理」の式と「ベルヌーイの式」の式を見比べてみよう。すると粘性摩擦に由来する項 ν∇⊗U と乱流による速度場の揺らぎに由来する項 〈u'⊗u'〉
が増えている。
ν∇⊗U の意味は流体の運動に伴う摩擦力で、「ゆがめる」変形(剪断応力)に対する抵抗である。ニュートン流体には変形した後で元に戻るような復元力はないので、流体は変形したまんまで戻らない*5のであり、ゆがめるのに使われた力はそのままエネルギー散逸してしまう。これを粘性損失という。
〈u'⊗u'〉はレイノルズ応力と呼ばれており、その意味は乱流による流体の「むだな動き」に由来する抵抗である。乱流ができると、流体は全体としては下流に向かって流れてはいるけれども、細かく見ていけばあっち行ったりこっち行ったりと迷走をしていて、流れとしては足踏みに近い状態になっている。つまり下流に向かって流そうとパイプにかけた圧力が、迷走する流体運動に持っていかれてしまい、100%下流向きには使われないということだ。これを乱流による圧力損失という。もちろん乱流でできた細かい渦どもは、最終的には粘性でブレーキがかかってエネルギー散逸を起こすことになるが、高レイノルズ数になるほど「粘性ブレーキ」よりも「迷走状態」の方がエネルギーのムダへの寄与は大きい。*6
ここで工学的、水理学的には、乱流による損失、粘性による損失はすべて「圧力のなかま」として扱われる。具体的には「管摩擦」「入口損失」等々(これらを「水頭 hydraulic head」と総称する)として扱い、ナビエ・ストークス方程式の初期値・境界値問題を解くことなく、ざっくりとした計算を経験値に基づいて実用的かつ確実に実行するノウハウが蓄積されている*7。
「答えが出ればいい」という人々にとっては、計算式の名称が「ベルヌーイの定理」でも「ベルヌーイの式」でもいいのかもしれない。実用的に正しい値が出れば、途中のロジックがウソであっても、思考の詰めが甘くても設計や評価に影響が無いからである。
さてRANSを管断面で積分して「ベルヌーイの式」を導出しよう。設定は半径 R, 管長 L の円筒形のパイプで、座標は (半径方向,周方向,軸方向) = ( r, θ, s ) とし、平均流
U = ( Ur(r,θ,s,t), Uθ(r,θ,s,t), Us(r,θ,s,t) ) = ( Ur(r,s), 0, Us(r,s) ),つまり軸対称な定常流れを仮定する*8。RANS の s 方向成分の式は
である。ここで揺らぎの2次の項も統計的に軸対称性を持つと仮定すると
∂s( P/ρ + g z + ( Ur2 + Us2 )/2 + 〈u's⊗u's〉) +
ν∂r( r ∂rUs )/r + ∂r( 〈u'r⊗u's〉 )
+
∂θ( 〈u'θ⊗u's〉/r )
= 0
これを管断面に関する平均値をとる
∂s( P/ρ + g z + ( Ur2 + Us2 )/2 + 〈u's⊗u's〉) +
ν∂r( r ∂rUs )/r + ∂r( 〈u'r⊗u's〉 )
= 0
これをさらに軸方向に積分して
(1/πR2)
∫0R
∫02π
[
∂s( P/ρ + g z + ( Ur2 + Us2 )/2 + 〈u's⊗u's〉) +
ν∂r( r ∂rUs )/r + ∂r( 〈u'r⊗u's〉 )
]
r dθ dr
= 0
↓
∂s( P/ρ + g z + ( Ur2 + Us2 )/2 + 〈u's⊗u's〉) + D + Tr
= 0
ここで
D = 2ν R (∂rUs)r=R,
Tr =
(2/R)〈u'r⊗u's〉r=R -
(2/R2)
∫0R
〈u'r⊗u's〉
dr
これよりベルヌーイの定理の式によく似た式が導かれた。
B(outlet) - B(inlet) +
∫inletoutlet( D + Tr ) ds
= 0,
ここで
B:= P/ρ + g z + ( Ur2 + Us2 )/2 + 〈u's⊗u's〉
ここで
- 管断面平均の速度( Ur2 + Us2 )/2 を流量の実測値から得られる速度 U に置き換え、
- 粘性や乱流による損失を「水頭」として inlet 側か outlet 側に(管路に沿った積分の計算ではなく)一括した値として「計上」する、具体的には実験的に得られた値(たとえば全開の球形バルブで係数が 10 で水頭が h=10U2/2g [m]*9)や経験式(管摩擦を求めるMoody図*10)に当てはめてる
ここで B の「境界値」をどうとるべきか考えよう。上記の式の導出はサイフォンのうちの「パイプ」の部分のみに着目した議論なのだが、パイプの「外」に物理量がどうつながるか簡単に考察する。
まず下流側の圧力だが、Miller and Comings, Ind. Eng. Chem., 1957, 49 (6), p.985 の乱流ジェットの実験によると、ジェット内部の静圧は負でその大きさは平均の運動量フラックス ρU2 の1/20程度であるという。同論文の図を見ると圧力をジェット中心の流速で規格化したもの P/ρUC2 のピーク値は -0.04 くらいである。これは種子田の解説記事『誤解の多いベルヌーイの定理』にある「自由噴流の圧力が至る所ほぼ大気圧に等しいという実験事実」という記述と首尾一貫しているように思われる。
つまり下流側の境界条件は、第ゼロ近似で周辺の静水圧 p, 第1近似で p - 0.05 ρU2 くらいと見積もれば良さそうである。流れ U の圧力への影響は小さい(つまりベルヌーイの「定理」で平均速度 U から P が概算できるような状況ではない)。
いまのサイフォンの問題だと P(outlet) + ρg z(outlet) 〜 patm と置くことになる。
次に上流側の圧力だが、静止流体が管口で U まで加速されている(加速する流れは乱流の生成が抑えられやすい(文献捜索中))、吸い込みなので流れの向きは出口側のジェットに比べるとかなり等方的にあちこちの向きから吸い込んでいるので(不安定性を起こすかく乱が流れに入ってきても、成長する前に管に入りそうなので)、乱流と粘性が管口近傍を除けば小さそうなので、大雑把にはベルヌーイの定理を使って B = ( p + ρgz + ρU2/2 )s=inlet = (一定) = patm + ρg H で見積もりを立てられそう。
[蛇足:ファインマンのスプリンクラー]上記の考察では吸い込みと吐き出しで境界条件の考え方が全然、異なっている。これはパイプの外の様子が全然、違うからである。これに似た例として、たしか『ご冗談でしょうファインマンさん』のどこかに、スプリンクラーを『吐き出し』ではなく『吸い込み』で動作させたらという問題を立てて、実験をしたら、実験装置を壊して叱られた…みたいな話があったように思う。
この問題はパイプの中の流れだけに注目すると、議論がドツボにはまる。パイプの内部の流れはレイノルズ数でほぼ決まるし、レイノルズ数はポンプの流量でほぼ決まるので、吸い込み、吐き出しで流れの向きが違うだけ、パイプ内部の流体の角運動量の絶対値に極端な差が出るわけがない。
この問題の「正解」は、吸い込み、吐き出しが外部の流体にどのような角運動量を与えているかに極端な差があるから(だから外部の流体に与えた角運動量の反作用としてのスプリンクラーの回転に差がある)。吐き出しの場合には細く狭い領域にジェットが形成されるが、吸い込みは吸い込み口の周辺のあらゆる方向から流体が流れ込むのでパイプの外の流体全体の角運動量は小さい。
[教訓] ファインマンのスプリンクラーもサイフォンも「管の内部」に注目をしてしまった結果、わけのわからない議論が百出してしまう。これを「木を見て森を見ず」という。自分自身への戒めとしたい。
[蛇足2]計算をやっていて気になったこと:Hagen-Poiseuille流を使った ρU2 の概算。
U(r) = Uc ( 1 - (r/R)2 ) を用いて、管断面内の平均速度を計算すると ∫∫U(r) r dr dθ/πR2 = Uc/2 となるから ρU2 = ρUc2/4 となる。
その一方で真面目に U2 の管断面平均を求めると ∫∫U(r)2 r dr dθ/πR2 = Uc2/3 となるから ρU2 = ρUc2/3 となり、17%くらい見積もりの値が変わってしまう。
これは「ベルヌーイの式」の各項の評価では平均流速を用いて運動量の流束 ρU2 (momentum flux)を評価しているが、流れのプロファイルによっては現実の運動量の流束の値よりも低く見積もることになっていることを示している。ここでは Hagen-Poiseuille 流を取ったので層流域の話なのだが、フラックスの17%のずれが概算として許容範囲なのかどうか実務経験がないのでイマイチよくわからない。[蛇足2ここまで]
[ベルヌーイの式のまとめ] 以上の RANS の平均化とその境界条件の考察から、サイフォンにおける圧力+重力 p + ρg z の分布の概形を考えると次のようになるだろう。
- 管の入口に吸い込まれるまでに、流体は加速されるので、圧力+重力はその分だけ減る。*11
- 管の内部では RANS の各項で決まる圧力損失が発生する。
- 管の出口の外側はほぼ周辺の圧力と同じ値になるが、吹き出しの中は速度成分を持つだけ少し低圧になっている(けれどもρU2に比べてかなり絶対値が小さいことが実験的に知られている)。
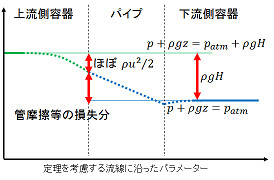
これを元に速度 u を概算するとすれば、大雑把には ρg H = ρu2/2 + [いろいろな損失] となる。この[いろいろな損失]の見積もりは工学、水理学の分野で実験的に確立している式や値を使う。例えば層流域で管摩擦だけが効くと仮定すれば ρg H = ρu2/2 + 32μL u / d2 を解くこととなる。
というわけで、「サイフォンはなぜ流れるのか」というところから遠く離れた、「サイフォンで流れる水の量はいくらか」という問題についての概観ができた。
松田先生のエントリの検討…はまた後ほど
上記の記事を書くのに冬休みの前半を使ってしまって、くたびれたので、松田先生のエントリの吟味はまた後日。松田先生のエントリには「正しい部分」と「不適切な部分」が混在し、錯綜しているので、慎重な応答が必要だからだ(例えば「鎖モデルとの対比」の部分で拘束力である張力と全エネルギー(ハミルトニアン)が一つの式に同居してたりして唖然とさせられたりする)。あらきの記述に対する正当な誤りの指摘(たとえばサイフォンの上流側の境界条件における流れの分の圧力低下)もあれば、不適切な引用(あらきの立式の前提を吟味しないままの引用)をして「あらきは誤り」と断じられて不愉快きわまりない部分もある。
感謝していることは、勉強のやり直しのきっかけをいただいたことである。
*1:種子田, 誤解の多い「ベルヌーイの定理」, 日本物理学会誌, Vol.50, No.12, 1995, p.972-973, http://ci.nii.ac.jp/naid/110002077058 この解説記事は「ベルヌーイの定理の前提を満たしていないのでダメ」と書かれている部分と「ベルヌーイの式をよい近似で使える」と書いてある部分が並存しているので、丁寧に読まないといけない。
*2:幾何学的形状から流れが事前に予測できる例としてはベンチュリー管も挙げられるだろうが、ここでは間違った説明も簡単に作れる例として挙げた。
*3:この図では低液面側の管口をわざと高液面側の管口より深く描いていて、管口の静水圧 p だけを見ると低液面側の方が高圧になるように設定してある。もちろん管の出入り口の深さがサイフォンの能力の計算に影響しないことを示すためである。
*4:乱流の統計理論ではよく「統計平均」が現れるが、平衡系の熱力学の基礎にあるような「規準となる(カノニカルな)アンサンブル」が確立しているわけでもない。
*5:ニュートン流体が変形の応力に対する復元力を持たないことを「水は方円の器に従う」と謂う。
*6:これは蛇足かもしれないが、高レイノルズ数の乱流に関する(少なくとも乱流理論の研究者で)知らぬ者のない未解決の問題として「乱流では動粘性係数ν→0の極限でエネルギー散逸率は有限値に留まる」という仮説がある。これは実験的に知られている結果から示唆されている仮説である。例えば Frisch, "Turbulence", Cambridge Univ. Press, 1995, Sect. 5.2 参照。これは非粘性のエネルギー保存則と矛盾しているように思えるが、Euler 方程式でエネルギー保存が証明できている「なめらかさ」には限界がある: Constantin, E, Titi, Comm. Math. Phys. Volume 165, Number 1 (1994), 207-209. 「細かい渦が次々にできるせいで」速度場の勾配 ∇u の値が発散してしまうんだろうと思われる。νがゼロに近づく極限を軽軽に非粘性と同一視はできない。
*7:これを「ナビエ・ストークス方程式を解いた」と称する感覚は、流体の理論研究の感覚とは違うなと感じる。
*8:平均流のs方向成分 Us のr方向の関数形は助走流から発達流へと下流に向けて変わるとする。このとき非圧縮性の条件よりr方向の速度成分が必要になる。
*9:例えば Kraus et al., "introduction to thermal and fluid enginnering", CRC Press, 2012, Boca Raton, p.532.
*11:この部分は理系学部の学部生のためのサイフォンの原理 - あらきけいすけの雑記帳でボクが見落としていた部分。この部分に注意を向けてくれたことを松田先生に感謝したい。